如果你有 python 或者 node 的命令行终端，或者浏览器里面的 Console，你可以做个测试，输入 0.3 + 0.6 看下值究竟是多少。

1
2
3
4
Welcome to Node.js v12.16.1.
Type ".help" for more information.
> 0.3+0.6
0.8999999999999999

32 bit 只能表示 2^32 次方个不同的数，大约 40 亿，看似已经很多了，但是比起无限多的实数集合却只是沧海一粟。

定点数的表示

定点数：固定小数点位置。比如假设 32 bit ，用 4 bit 来表示 0 ~ 9 的整数，那么可表示 8 个整数，我们把后面两个整数，当成小数部分，把前面 6 个整数当成整数部分，那么 32 bit 可表示 0 到 999999.99 这样 1 亿个实数了。

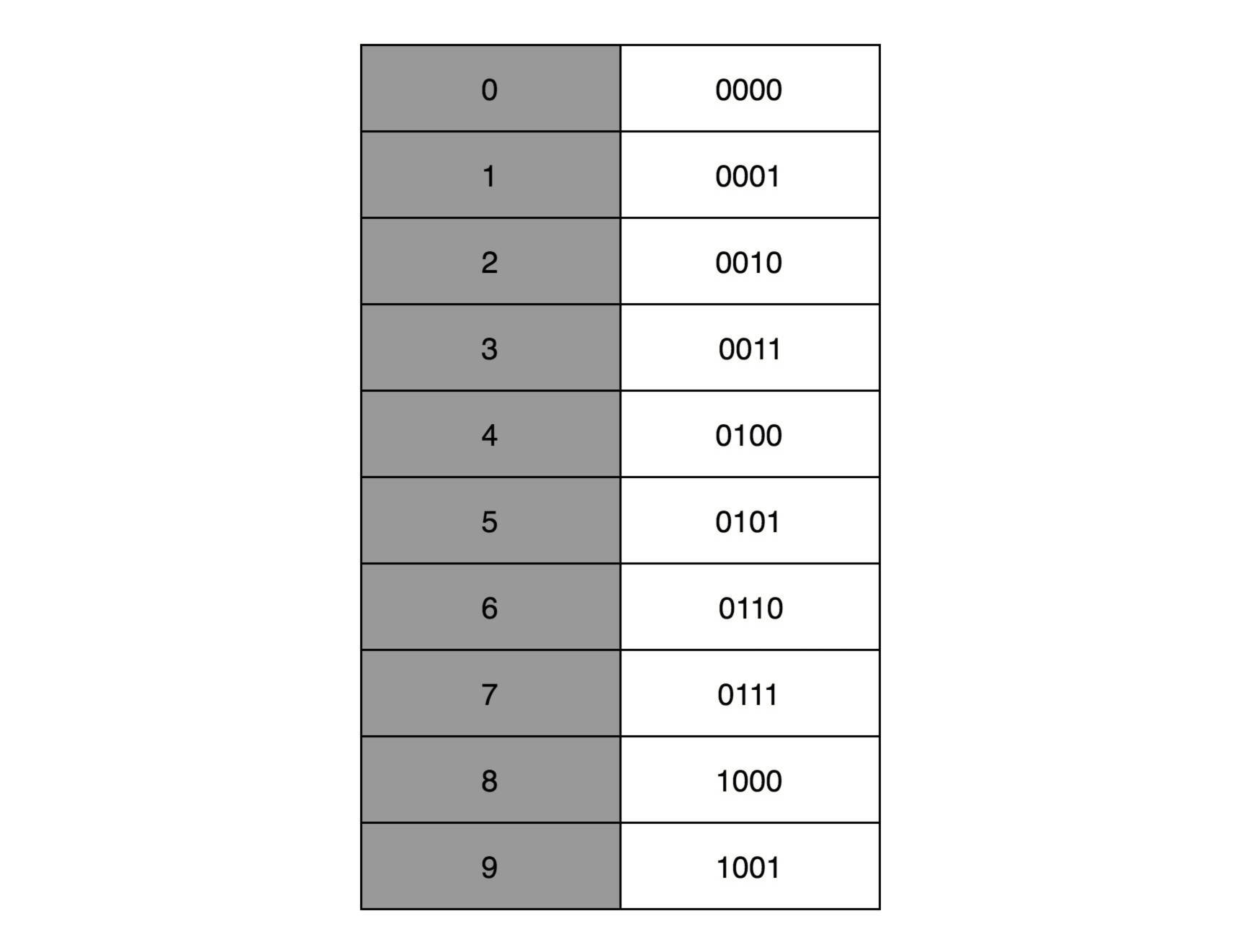
这种用二进制表示十进制的编码方式，叫作 BCD 编码（Binary-Coded Decimal），最常用的是在超市、银行这样需要用小数记录金额的情况里。在超市里面，我们的小数最多也就到分。

不过，这样的表示方式也有几个缺点。

  1. 空间浪费。本来 32 个比特我们可以表示 40 亿个不同的数，但是在 BCD 编码下，只能表示 1 亿个数，如果我们要精确到分的话，那么能够表示的最大金额也就是到 100 万。

  2. 没办法同时表示很大的数字和很小的数字。

这时就需要浮点数来表示了。

浮点数的表示

生活中，我们会用科学计数法来表示这个很大的数字，比如 1.0* 10^82，而不需要写 82 个 0。

在计算机里，可以用一样的科学计数法来表示实数。有一个 IEEE 的标准，定义了两个基本的格式。一个是用 32 比特表示单精度的浮点数，也就是 float 或者 float32 类型。另外一个是用 64 比特表示双精度的浮点数，也就是 double 或者 float64 类型。

双精度类型和单精度类型差不多，这里，我们来看单精度类型。

浮点数的组成

单精度的 32 个比特可以分成三部分

  1. 符号位，用来表示是正数还是负数。我们一般用 s 来表示。
  2. 一个 8 个比特组成的指数位。我们一般用 e 来表示。能表示的整数范围在 0 ~ 255
  3. 一个 23 个比特组成的有效数位。我们用 f 来表示。

浮点数前辈们定义了这样一个公式

(−1)^s × 1.f × 2^e

在这样的浮点数表示下，不考虑符号的话，浮点数能够表示的最小的数和最大的数，差不多是 1.000… ^ (2^-126) ≈ 1.17×10^38 和1.9999999… ^(2^127) ≈ 3.40×10^38。比前面的 BCD 编码能够表示的范围大多了。

浮点加法数精度丢失问题

浮点数的加法过程，当指数位较小的数，需要在有效位进行右移，在右移的过程中，最右侧的有效位就被丢弃掉了。这会导致对应的指数位较小的数，在加法发生之前，就丢失精度。

32 位浮点数的有效位长度一共只有 23 位，如果两个数的指数位差出 23 位，较小的数右移 24 位之后，所有的有效位就都丢失了。这也就意味着，虽然浮点数可以表示上到 3.40×10^38，下到 1.17×10^−38 这样的数值范围。但是在实际计算的时候，只要两个数，差出 2^24，也就是差不多 1600 万倍，那这两个数相加之后，结果完全不会变化。

下面用一个简单的 Java 程序，让一个值为 2000 万的 32 位浮点数和 1 相加，你会发现，+1 这个过程因为精度损失，被“完全抛弃”了。

1
2
3
4
5
6
7
8
9
10
11
12
13

public class FloatPrecision {
  public static void main(String[] args) {
    float a = 20000000.0f;
    float b = 1.0f;
    float c = a + b;
    System.out.println("c is " + c);
    float d = c - a;
    System.out.println("d is " + d);
  }
}
// c is 2.0E7
// d is 0.0

有没有什么办法来解决这个精度丢失问题呢？

聪明的计算机科学家们也想出了具体的解决办法。他们发明了一种叫作 Kahan Summation 的算法来解决这个问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

public class KahanSummation {
  public static void main(String[] args) {
    float sum = 0.0f;
    float c = 0.0f;
    for (int i = 0; i < 20000000; i++) {
      float x = 1.0f;
      float y = x - c;
      float t = sum + y;
      c = (t-sum)-y;
      sum = t;      
    }
    System.out.println("sum is " + sum);   
  }  
}
// sum is 2.0E7

原理其实并不复杂，就是在每次的计算过程中，都用一次减法，把当前加法计算中损失的精度记录下来，然后在后面的循环中，把这个精度损失放在要加的小数上，再做一次运算。

总结

虽然浮点数能够表示的数据范围变大了很多，但是在实际应用的时候，由于存在精度损失，会导致加法的结果和我们的预期不同，乃至于完全没有加上的情况。

所以，一般情况下，在实践应用中，对于需要精确数值的，比如银行存款、电商交易，我们都会使用定点数或者整数类型。比方说，你一定在 MySQL 里用过 decimal(12,2)，来表示订单金额。如果我们的银行存款用 32 位浮点数表示，就会出现，马云的账户里有 2 千万，我的账户里只剩 1 块钱。结果银行一汇总总金额，那 1 块钱在账上就“不翼而飞”了。

浮点数，则更适合我们不需要有一个非常精确的计算结果的情况。比如，从我家到办公室的距离，就不存在一个 100% 精确的值。我们可以精确到公里、米，甚至厘米，但是既没有必要、也没有可能去精确到微米乃至纳米。