计算机最重要的是 CPU，除此之外，第二重要的就是内存，内存属于计算机五大组成部分中的存储器，我们的指令和数据，都要先加载到内存，才会被 CPU 拿去执行。

之前有篇提到过，程序并不能直接访问物理内存，而是通过虚拟内存地址转换到物理内存地址，从而加载数据，那么虚拟地址究竟如何转换成物理内存地址的呢？

简单页表

最简单的方法，就是建立一张映射表，计算机里面叫页表。页表可以编号，我们其实只需保存虚拟地址的页号与物理地址页号之间的映射，同时虚拟地址需要携带偏移量，这样我们就可根据内存地址找到页号，在根据偏移量定位到具体物理地址。

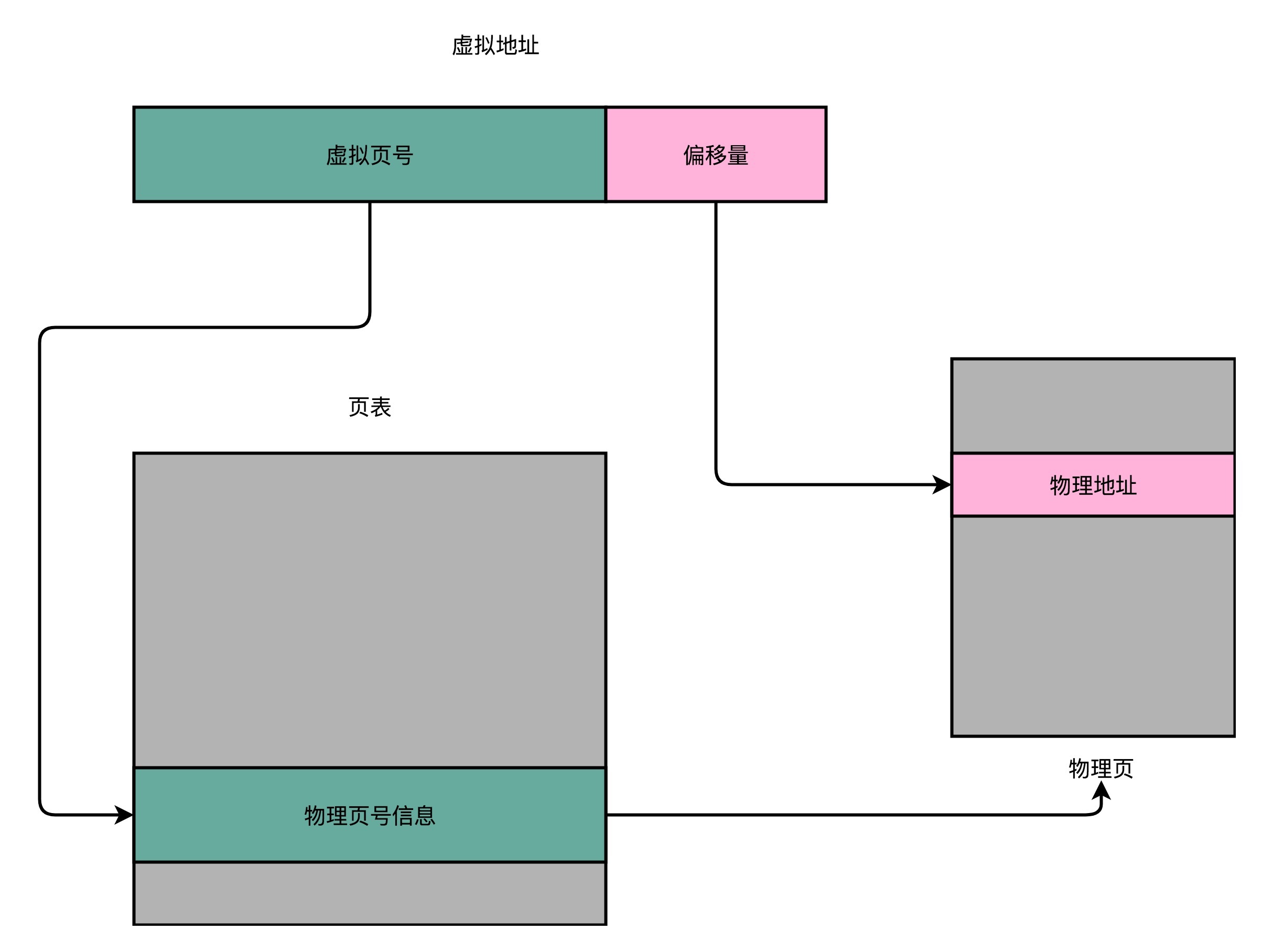
总结一下，对于一个内存地址转换，其实就是这样三个步骤：

  1. 把虚拟内存地址，切分成页号和偏移量的组合
  2. 从页表里面，查询出虚拟页号，对应的物理页号
  3. 直接拿物理页号，加上前面的偏移量，就得到了物理内存地址

这种简单页表容易理解，但是有个问题，内存占用比较大。

以一个页的大小是4K字节（4KB）为例，我们需要20位的高位，12位的低位。32位的内存地址空间，页表一共需要记录2^20个到物理页号的映射关系。这个存储关系，就好比一个2^20大小的数组。一个页号是完整的32位的4字节（Byte），这样一个页表就需要4MB的空间。如果每一个进程都有这样一个页表，内存占用就更大了。

为解决这个问题，我们采用的是一种叫作多级页表（Multi-Level Page Table）的解决方案。

多级页表

多级页表就像一个多叉树的数据结构，所以我们常常称它为页表树（Page Table Tree）。因为虚拟内存地址分布的连续性，树的第一层节点的指针，很多就是空的，也就不需要有对应的子树了。所谓不需要子树，其实就是不需要对应的2级、3级的页表。找到最终的物理页号，就好像通过一个特定的访问路径，走到树最底层的叶子节点。

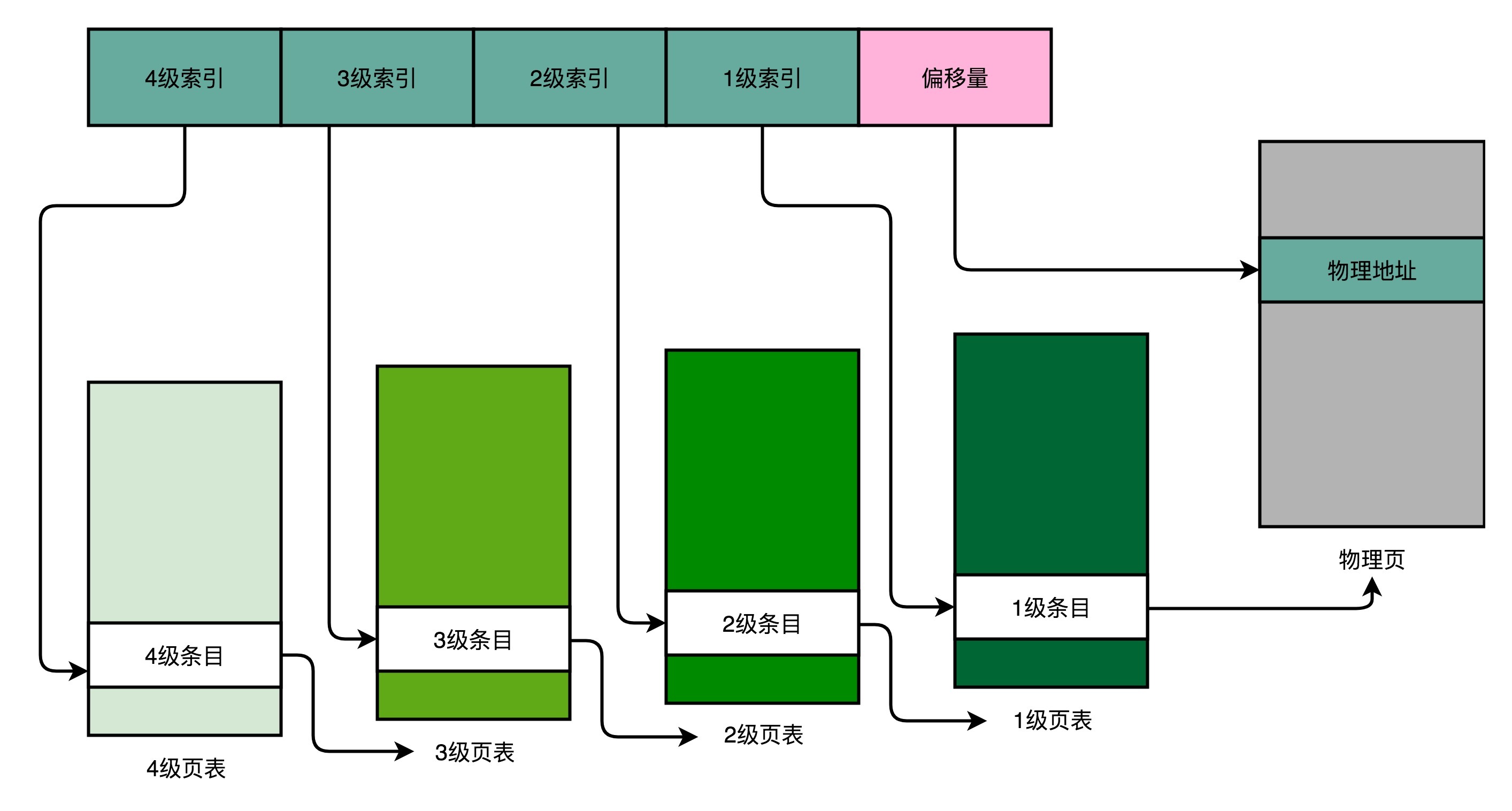
以这样的分成4级的多级页表来看，每一级如果都用5个比特表示。那么每一张某1级的页表，只需要2^5=32个条目。如果每个条目还是4个字节，那么一共需要128个字节。而一个1级索引表，对应32个4KB的也就是128KB的大小。一个填满的2级索引表，对应的就是32个1级索引表，也就是4MB的大小。

我们可以一起来测算一下，一个进程如果占用了8MB的内存空间，分成了2个4MB的连续空间。那么，它一共需要2个独立的、填满的2级索引表，也就意味着64个1级索引表，2个独立的3级索引表，1个4级索引表。一共需要69个索引表，每个128字节，大概就是9KB的空间。比起4MB来说，只有差不多1/500。

多级页表它其实是一个“以时间换空间”的策略。原本我们进行一次地址转换，只需要访问一次内存就能找到物理页号，算出物理内存地址。但是，用了4级页表，我们就需要访问4次内存，才能找到物理页号了。